Section: Scientific Foundations

Approximation methods

All the mathematical models considered and studied in Smash consist in hyperbolic systems of PDE's. Most of the attention is focused on the 7 equation model for non-equilibrium mixtures and the 5 equation model for mechanical equilibrium mixtures. The main difficulty with these models is that they cannot be written under divergence form. Obviously, the conservation principles and the entropy inequality are fulfilled, but some equations (the volume fraction equation in particular) cannot be cast under conservative form. From a theoretical point of view, it is known since the works of Schwartz [45] that the product of two distributions is not defined. Therefore, the question of giving a sense to this product arises and as a consequence, the numerical approximation of non-conservative terms is unclear [25] , [34] . Aware of this difficulty, we have developed two specific methods to solve such systems.

The first one is the discrete equations method (DEM) presented previously as a new homogenization method. It is moreover a numerical method that solves non-conservative products for the 7 equation model in the presence of shocks. With this method, Riemann problem solutions are averaged in each sub-volume corresponding to the phase volumes in a given computational cell. When a shock propagates inside a cell, each interaction with an interface, corresponds to the location where non-conservative products are undefined. However, at each interaction, a diffraction process appears. The shock discontinuity splits in several waves : a left facing reflected wave, a right facing transmitted wave and a contact wave. The interface position now corresponds to the one of the contact wave. Along its trajectory, the velocity and pressure are now continuous : this is a direct consequence of the diffraction process. The non-conservative products that appear in these equations are precisely those that involve velocity, pressure and characteristic function gradient. The characteristic function gradient remains discontinuous at each interface (it corresponds to the normal) but the other variables are now continuous. Corresponding non-conservative products are consequently perfectly defined : they correspond to the local solution of the Riemann problem with an incoming shock as initial data. This method has been successfully developed and validated in many applications [1] , [8] , [6] , [24] .

The second numerical method deals with the numerical approximation of the five equation model. Thanks to the shock relations previously determined, there is no difficulty to solve the Riemann problem. However, the next step is to average (or to project) the solution on the computational cell. Such a projection is not trivial when dealing with a non-conservative variable. For example, it is well known that pressure or temperature volume average has no physical meaning. The same remark holds for the cell average of volume fraction and internal energy. To circumvent this difficulty a new relaxation method has been built [43] . This method uses two main ideas.

The first one is to transform one of the non-conservative products into a relaxation term. This is possible with the volume fraction equation, where the non conservative term corresponds to the asymptotic limit of a pressure relaxation term. Then, a splitting method is used to solve the corresponding volume fraction equation. During the hyperbolic step, there is no difficulty to derive a positivity preserving transport scheme. During the stiff relaxation step, following preceding analysis of pressure relaxation solvers [5] , there is no difficulty neither to derive entropy preserving nor positive relaxation solvers.

The second idea deals with the management of the phase's energy equations, which are also present under non-conservative form. These equations are able to compute regular/smooth solutions, such as expansion waves, but are inaccurate for shocks. Thus they are only used at shocks to predict the solution. With the predicted internal energies, phase's pressures are computed and then relaxed to equilibrium. It results in an approximation of the volume fraction at shocks. This approximation is then used in the mixture equation of state, that is unambiguously determined. This equation of state is based on the mixture energy, a supplementary equation. This equation, apparently redundant, has to be fulfiled however. Its numerical approximation is obvious even in the presence of shocks since it is a conservation law. With the help of the mixture energy and predicted volume fraction, the mixture pressure is now computed, therefore closing the system. This treatment guarantees correct, convergent and conservative wave transmission across material interfaces separating pure media. When the interface separates a fluid and a mixture of materials, the correct partition of energies among phases is fulfiled by replacing at the shock front the internal energy equations by their corresponding jumps [44] . To ensure the numerical solution strictly follows the phase's Hugoniot curves, the poles of these curves are transported [41] . With this treatment, the method also converges for multiphase shocks.

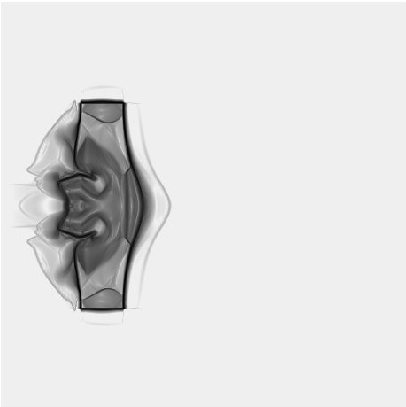
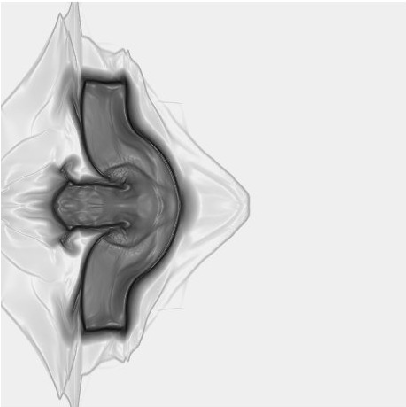
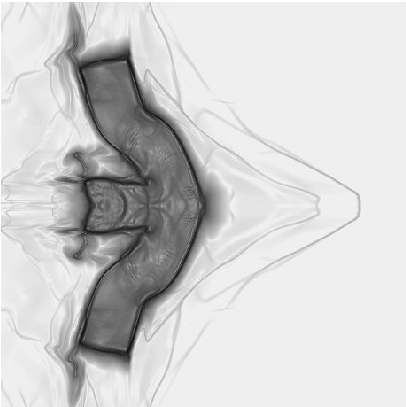
This method is very efficient and simple to implement. This also helped us considerably to solve very large systems of hyperbolic equations, like those arising for elastic materials in large deformations. The fluid-solid coupling via diffuse interfaces with extreme density ratios was done efficiently, as shown in figure 5 .

Figure 5. A copper projectile impacts a copper plate at the velocity of 800 m/s. Both materials are considered compressible and elastic, and are surrounded by air at atmospheric pressure.

Another difficulty encountered in solving two-phase flow problems comes from the high disparity between the wave speeds of each existing fluid material. In particular, one of the fluids may be very close to the incompressibility limit. In that case, we face up the problem of very low Mach number flows. The numerical treatment of these flows is still a problem and involves non trivial modifications of the original upwind schemes [33] , [32] . Our investigations in that domain concern both acoustic and incompressible aspects in methodologies for setting up suitable numerical methods.